Program realizowany przez:
"Giełda”- gra z zastosowaniem procentów
Autor/Autorka: Sylwia Marcinkowska
Szkoła: Gimnazjum w Sochaczewie
Ekspert CEO: Jerzy Kielech (eksperta wyróżniono kolorem)
|
Temat: |
Giełda”- strategiczna gra z zastosowaniem procentów |
|
Podstawowe pojęcia: |
Obliczenia procentowe, zaokrąglanie liczb, działania na liczbach wymiernych, obniżki, podwyżki |
| Źródło: |  Nauczycielka napisała, że poznała pomysł gry na szkoleniu; brak dokładniejszych informacji. Nauczycielka napisała, że poznała pomysł gry na szkoleniu; brak dokładniejszych informacji. |
| Planowane korzyści z gry | Przećwiczenie umiejętności wykonywania obliczeń z zastosowaniem procentów, (podwyżka, obniżka), doskonalenie działań na liczbach wymiernych oraz zaokrąglanie liczb. |
| Instrukcja gry |
1. Uczniowie zostają podzieleni na grupy 4-5 osobowe . |
| Opis strategii jaką obrali uczniowie | 
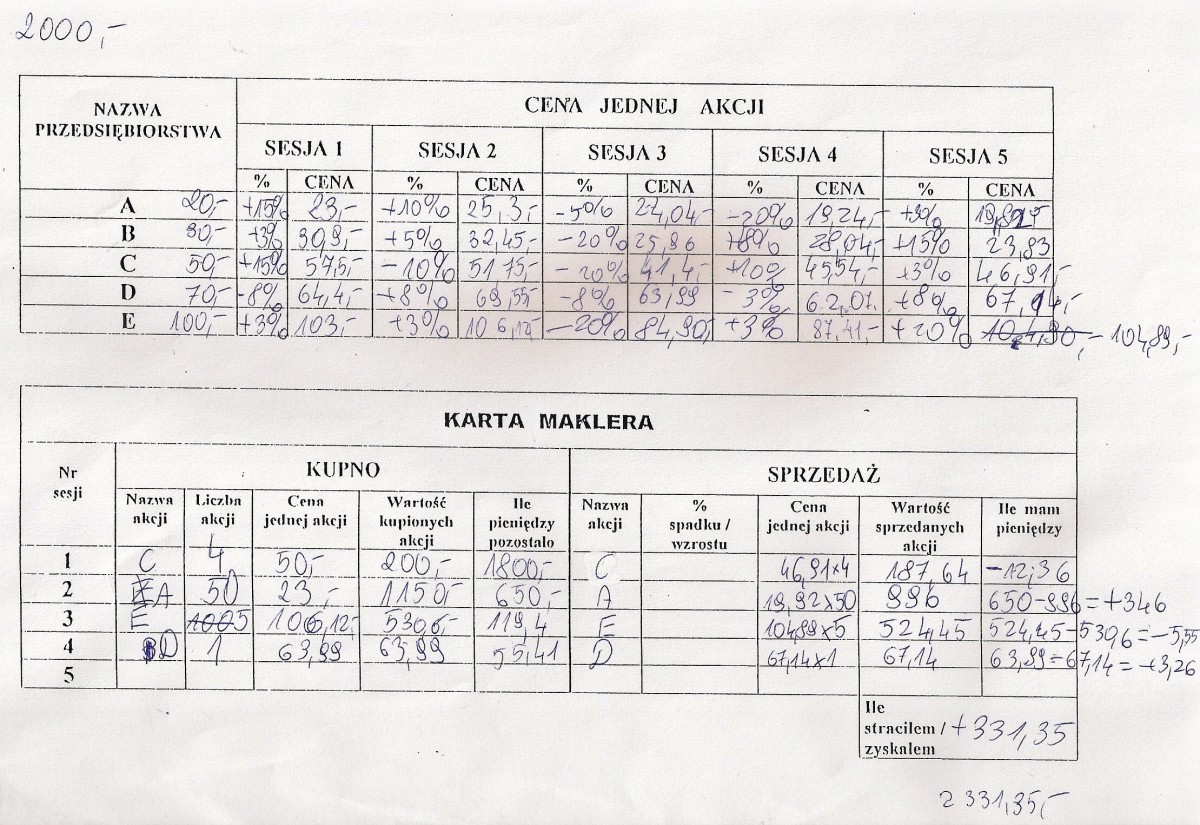
Gra wg zaproponowanej instrukcji nie jest grą strategiczną, gdyż o powodzeniu (ostatecznym zysku na giełdzie) decyduje los.
|
| Propozycja modyfikacji gry | 
W grze można modyfikować:
- kwotę przeznaczoną na zakup akcji, Ambitnym zadaniem dla konstruktorów gry zbudowanej na tej zasadzie byłoby wymyślenie sposobu na możliwość wpływu strategicznego na jej wynik. Uczniowie mogliby np. proponować różne poziomy procentowe (w wyznaczonym zakresie) dla poszczególnych firm przed każdą sesją i ustalać je jako średnią propozycji. Mieliby wówczas wpływ na wzrosty i spadki. Grę można także urozmaicić prowadząc po każdej sesji giełdę akcji, które inni zaproponowaliby do odsprzedaży. |
| Rekomendacja |
Zaletą tej gry są oczywiste korzyści dydaktyczne; uczniowie ćwiczą obliczanie zysków i strat obliczając procent danej liczby, stosują zaokrąglenia, doskonalą działania na liczbach wymiernych i sprawność rachunkową. |
| Dodatkowe informacje dla nauczycieli naśladowców | 
Prawidłowo przeprowadzona gra miała pokazać/ nauczyć: - obliczania procentu danej liczby, |
| Podstawa programowa |
Wymagania szczegółowe 1. Liczby wymierne dodatnie. Uczeń: 5. Procenty. Uczeń: |
| Podstawa programowa | 
Wymagania ogólne:
I. Sprawność rachunkowa. |
|
|
|