Program realizowany przez:
Suma kątów w wielokącie
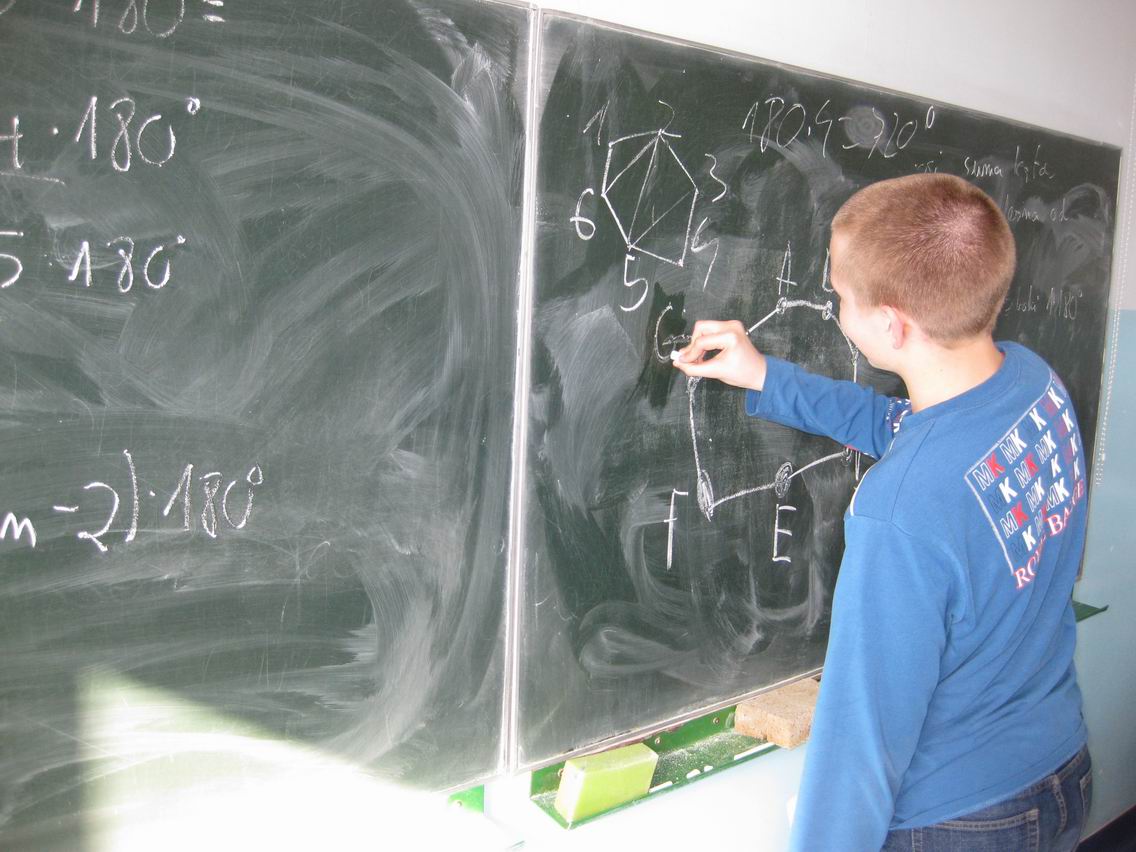
Autor: Łukasz Mrowicki
Rekomendacja konsultanta merytorycznego CEO, Jerzego Kielecha:
To doświadczenie podpatrzone przez uczniów w podręczniku matematyki, dzięki zaproponowanej instrukcji jest przykładem prostych zajęć z pytaniem problemowym.
Podstawowe pojęcia:
Wielokąt, kąt wewnętrzny wielokąta, wyrażenie algebraiczne
Źródło:
Podręcznik matematyki „Matematyka 1, GWO” str. 105 oraz str. 113
Hipoteza zaproponowana przez uczniów:
- Suma kątów w wielokącie o „n” bokach wynosi n*180o
- (n-2)*180o
Opis doświadczenia:
„Uczniowie mają za zadanie przeanalizować ile wynosi suma katów wewnętrznych rysowanych wielokątów, których ilość boków zwiększa się stopniowo o jeden Każdorazowo należy podzielić powstały wielokąt na rozłączne trójkąty w ten sposób by wypełniły cały wielokąt (rysując odpowiednie przekątne wyprowadzone z jednego wierzchołka) i zliczyć sumę kątów przy znanej sumie dla trójkąta. Problemem do rozwiązania jest określenie wyrażenia algebraicznego określającego ogólna zależność między sumą katów a ilością boków z wykorzystaniem zasady. Iż suma katów trójkąta jest stała”
Zmienne występujące w doświadczeniu
Jakie zmienną/wielkość będziemy zmieniać? (zmienna niezależna)
Liczba boków w wielokącie („n” w „n- kącie”)
Jaką zmienną/wielkość będziemy mierzyć - obserwować? (zmienna zależna)
Suma kątów wewnętrznych wielokąta. (Jakim wyrażeniem arytmetycznym można określić tę sumę dla danego wielokąta, jakim wyrażeniem da się opisać sumę w zależności od n.)
Czego w naszym eksperymencie nie będziemy zmieniać? (zmienne kontrolne)
Trójkąty muszą być rozłączne i wypełnić cały wielokąt. Podział musi gwarantować, że suma wszystkich katów trójkąta równa jest sumie katów wielokąta.
Instrukcja do doświadczenia:
Instrukcja.
- Rysujemy dowolny trójkąt i wnioskujemy, że suma kątów wynosi 180o.
- Rysujemy dowolny czworokąt i „dzielimy” go na dwa trójkąty. Wnioskujemy, że suma katów w czworokącie wynosi 2*180o=360o.
- Rysujemy dowolny pięciokąt i „dzielimy” go na trójkąty. Wyciągamy wniosek co do sumy katów wewnętrznych.
- Rysujemy dowolny sześciokąt i „dzielimy” go na trójkąty. Wyciągamy wniosek co do sumy katów wewnętrznych.
- Tworzymy ogólne wyrażenie algebraiczne służące do obliczenia sumy kątów wewnętrznych w wielokącie o „n”- bokach.
BHP.
Ostrożnie posługiwać się przyborami na tablicy.
Proponowany sposób dokumentacji uczniowskiej:
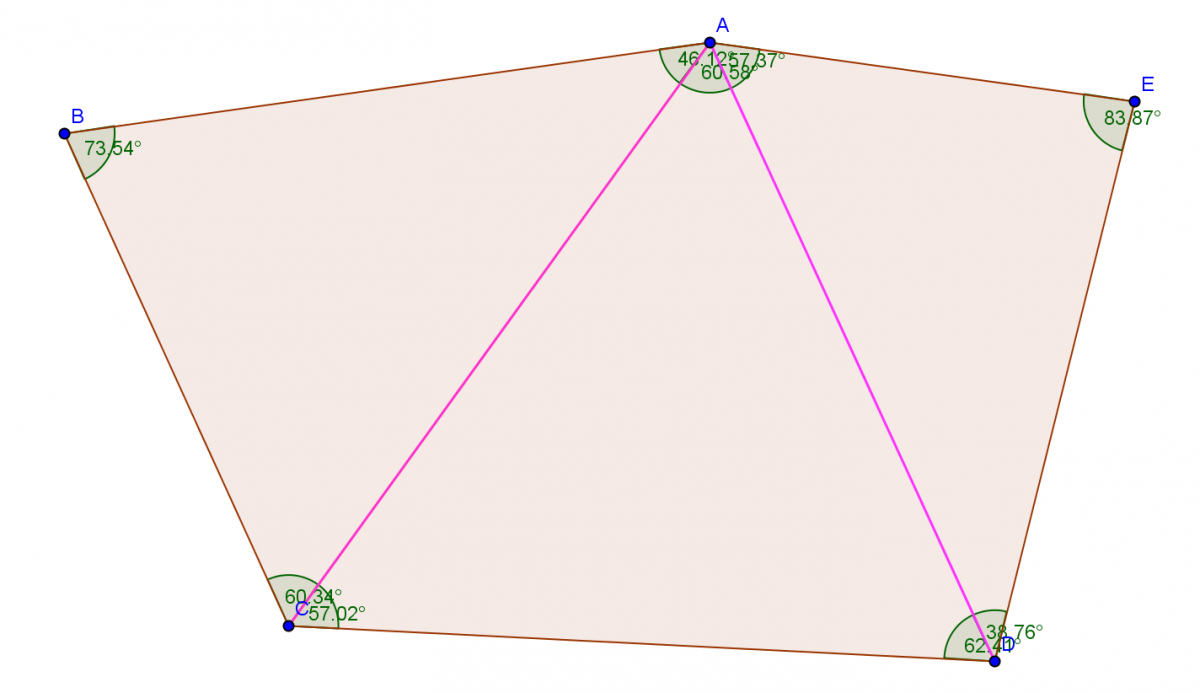
Powstają rysunki kolejnych wielokątów i podział na trójkąty wg opisanej zasady np. w sposób zaproponowany z wykorzystaniem programu komputerowego
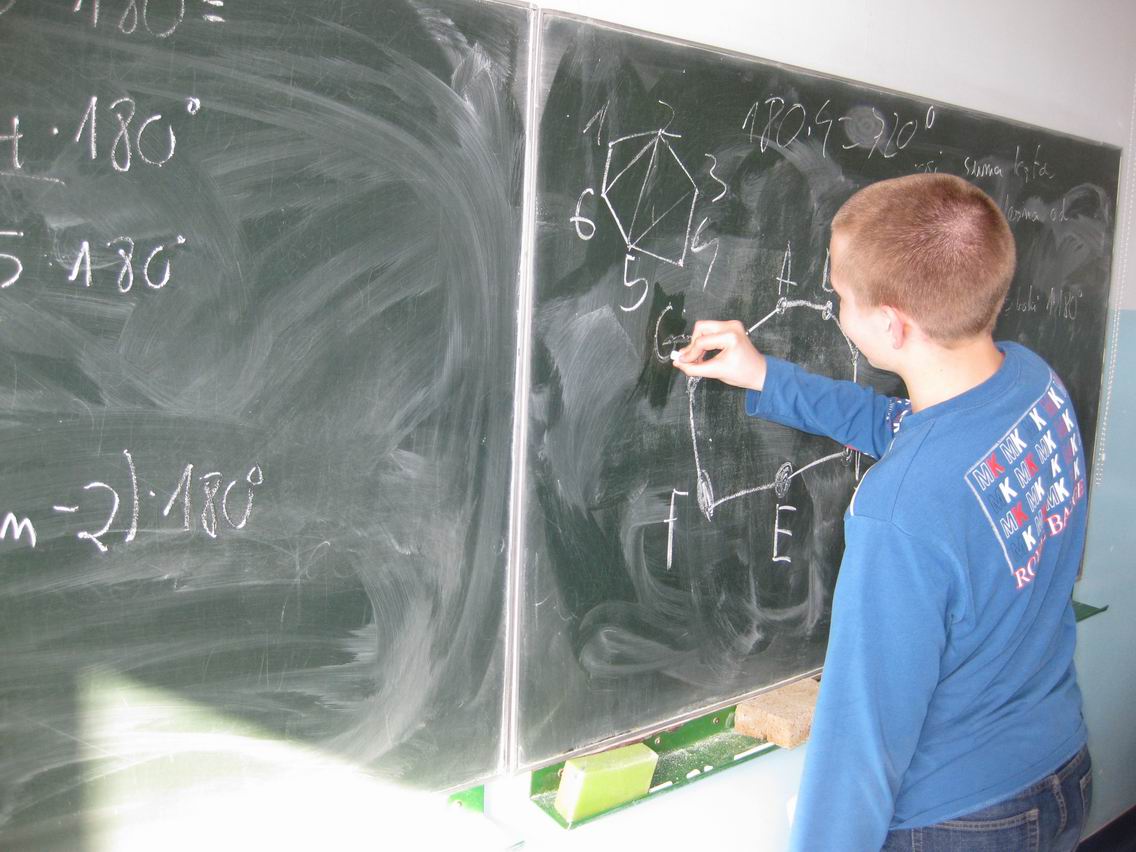
Uczniowie zapisują sumy katów w kartach pracy i okrywają ogólną zależność – powstaje odpowiednie wyrażenie algebraiczne
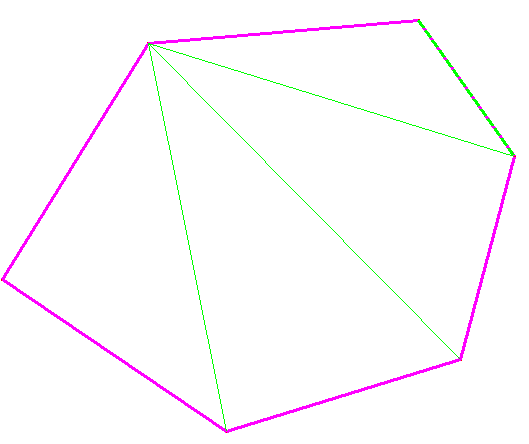
Można zaproponować drobną modyfikację instrukcji doświadczenia; na obserwację o ile zmienia się ilość trójkątów na które został podzielony w oparciu o rysunek, który przekształcamy dynamicznie w programie komputerowym.
Istnieje możliwość nie narzucania rozumowania związanego z podziałem na trójkąty, ale wyłącznie „pomiar” (komputerowy) sumy kątów po zmianie ilości boków. Uczniowie po zauważeniu prawidłowości, że każdorazowo suma wzrasta o 180o , nie znając opisanej zasady podziału wielokąta na trójkąty, najpierw są w stanie zbudować poprawnie wyrażenie algebraiczne, a następnie – poprzez skojarzenie tej zmiany z sumą kątów trójkąta, mogą poszukiwać geometrycznego uzasadnienia odkrytej prawidłowości. Wymaga to zmiany instrukcji stosownie do opisanej koncepcji.
Podstawa programowa:
Cele kształcenia (wymagania ogólne):
- modelowanie matematyczne - uczeń dobiera lub buduje model matematyczny prostej sytuacji,
- użycie i tworzenie strategii - uczeń stosuje strategię jasno wynikającą z treści zadania lub tworzy strategię rozwiązania problemu,
Treści nauczania (wymagania szczegółowe):
6. Wyrażenia algebraiczne. Uczeń:
1) opisuje za pomocą wyrażeń algebraicznych związki między różnymi wielkościami;
2) oblicza wartości liczbowe wyrażeń algebraicznych;
10. Figury płaskie. Uczeń:
8) korzysta z własności kątów i przekątnych w prostokątach, równoległobokach, rombach i w trapezach;



