Matematyka a ochrona środowiska

Matematyka a ochrona środowiska

Jednym z  elementów ochrony środowiska naturalnego jest segregacja i właściwe składowanie  odpadów, w szczególności, pochodzących z naszych gospodarstw domowych, opakowań szklanych, plastikowych i papierowych. Tematem tym zajęli się uczniowie Gimnazjum w Lelisie , którzy pod opieką nauczycielki Jolanty Olkowskiej przygotowali, podczas  zajęć SKN realizowanych w ramach programu Akademia Uczniowska,. opisane poniżej doświadczenie.

 

Rekomendacja eksperta CEO  Włodzimierza Gapskiego

Ciekawa propozycja zajęć z interesującym pytaniem problemowym. Proste doświadczenia pozwala zrozumieć jak istotne, oprócz selektywnej zbiórki odpadów,  jest odpowiednie przygotowanie opakowań do składowania w pojemnikach na odpady komunalne.  Doświadczenie może być modyfikowane na różne sposoby, a pomiary i obliczenia mogą dotyczyć innych rodzajów opakowań, na przykład plastikowych butelek lub puszek po napojach.

Temat zajęć- pytanie problemowe

Ile razy mniej przestrzeni zajmie zgniecione pudełko po mleku?

Podstawowe pojęcia

• objętość prostopadłościanu
• jednostki objętości
• „ile razy mniej”

Źródło:

Pomysł własny uczniów

Hipoteza sformułowana przez uczniów:

Zgniecione pudełko zajmie około 7 razy mniej przestrzeni niż wyrzucone bez zgniecenia.

Opis doświadczenia:

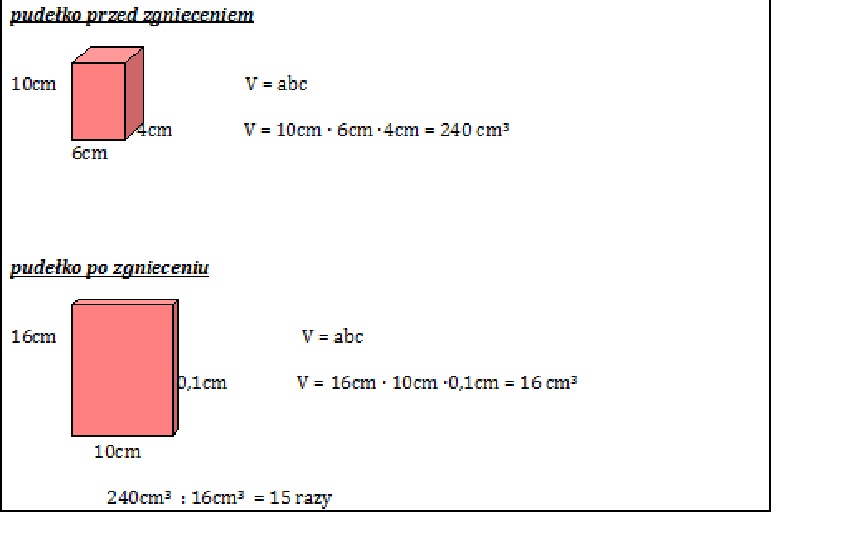
Doświadczenie polega na obliczeniu objętości pudełka po mleku przed zgnieceniem i po zgnieceniu i porównaniu, ile razy mniejszą objętość  ma pudełko zgniecione, aby lepiej zrozumieć potrzebę porządkowania odpadów.

Instrukcja do doświadczenia

Kolejne czynności uczniów

1. zmierzyć wymiary pudełka prostopadłościennego, np. po mleku
2. obliczyć objętość pudełka
3. zgnieść pudełko „na płasko”
4. zmierzyć wymiary zgniecionego pudełka, obliczyć objętość
5. obliczyć, ile razy mniej przestzeni zajmuje zgniecione pudełko.

Wnioski z doświadczenia

Czy wyniki doświadczenia są zgodne z hipotezą?               NIE    

Uzasadnienie: Wyniki okazały się niezgodne z hipotezą, ponieważ zgniecione pudełko zajmowało 15 razy mniej przestrzeni, a nie 7 razy. Czyli około dwa razy mniej niż założyliśmy. To daje nam do myślenia, na temat segregacji śmieci.

Podstawa programowa

Matematyka

1.   Liczby wymierne dodatnie. Uczeń:

• dodaje, odejmuje, mnoży i dzieli liczby wymierne zapisane w postaci ułamków zwykłych lub rozwinięć dziesiętnych skończonych zgodnie z własną strategią obliczeń (także z wykorzystaniem kalkulatora);
• oblicza wartości nieskomplikowanych wyrażeń arytmetycznych zawierających ułamki zwykłe i dziesiętne;

2. Bryły. Uczeń:

• oblicza pole powierzchni i objętość graniastosłupa prostego, ostrosłupa, walca, stożka, kuli (także w zadaniach osadzonych w kontekście praktycznym);

Komentarz eksperta

Analizując złączony do sprawozdania z zajęć fragment dokumentacji uczniowskiej można mieć wątpliwość, czy realne jest zgniecenie w domowych ( szkolnych) warunkach pudełka po mleku do grubości 1 mm.  Poza tym, łatwo zauważyć, że zgniecione pudełko nie ma kształtu prostopadłościanu, stąd trudno przyjąć objętość takiej bryły, jako przestrzeń, którą zajmuje zgniecione pudełko. Sytuacja ta stwarza okazję do przeprowadzenia z uczniami dyskusji na temat szacowania objętości otrzymanej po zgnieceniu bryły. Weryfikację poprawności wyniku może stanowić doświadczenie polegające na wypełnianiu większego pojemnika
o znanej objętości zgniecionymi kartonami. Następnie możemy obliczyć ilość nie zgniecionych kartonów, które może zmieścić ten pojemnik, a na koniec porównać oba wyniki i jeszcze raz udzielić odpowiedzi na pytanie problemowe zawarte w temacie zajęć.

Nie mniej interesujące dla uczniów może być podobne doświadczenie, połączone ze zgniataniem plastikowych butelek o różnym kształcie lub puszek po napojach. W tym przypadku dodatkowa trudność wiąże się z obliczeniem lub znalezieniem sposobu na  wyznaczenie objętości opakowania przed zgnieceniem 

Opracował Włodzimierz Gapski