Czy można huśtać się ze słoniem?

Powyższe pytanie problemowe było tematem lekcji przygotowanej i przeprowadzonej przez uczniów podczas  zajęć SKN realizowanych w ramach kursu Eksperymentowanie i wzajemne nauczanie pod opieką Joanny Herman -  nauczycielki matematyki w   Gimnazjum nr 2 w Olsztynie.

 

Rekomendacja eksperta CEO  Włodzimierza Gapskiego: Zaproponowany przez uczniów eksperyment fizyczny do zilustrowania i wyjaśnienia pojęcia matematycznego (proporcjonalność odwrotna), to  oryginalny i interesujący pomysł, a jednocześnie bardzo dobry przykład integracji międzyprzedmiotowej. Realizując doświadczenie uczniowie odkrywają, że  siła przyłożona do dźwigni dwustronnej jest odwrotnie proporcjonalna do długości jej ramienia. Bardzo ciekawe i atrakcyjne dla uczniów, choć być może niezbyt precyzyjne ( o jaką huśtawkę chodzi?) jest pytanie problemowe „Czy można huśtać się ze słoniem?”. Inspiracją do pomysłu na zajęcia było zadanie z podręcznika GWO do matematyki dla klasy I.

 

Temat zajęć- pytanie problemowe: Czy można huśtać się ze słoniem?

 

Źrodło: Podręcznik Matematyka dla klasy 1 gimnazjum. GWO

 

Hipoteza sformułowana przez uczniów: Możemy huśtać się ze słoniem, jednak przy odpowiednich odległościach

 

Opis doświadczenia:

Instrukcja do doświadczenia przygotowana przez uczniów ( fragment karty pracy)

  1. Weź linijkę, przedmiot o znanej masie do 50 g i długopis/ołówek. Na linijce z jednej strony połóż przedmiot o znanej masie, a po przeciwnej długopis. Linijkę umieść na brzegu stołu i delikatnie przesuwaj do momentu aż się przechyli. Odczytaj wtedy na linijce odległość od brzegu stołu do przedmiotu o znanej masie.
  2. Oblicz korzystając ze wzoru masę długopisu.

m*r=M*R       

 m –waga długopisu,

M – waga przedmiotu (o znanej masie)

 r – odległość długopisu od brzegu stołu,

R - odległość przedmiotu o   znanej masie od brzegu stołu

  1. Podobnie oblicz wagę innego przedmiotu;
  2. Przyjmij, że człowiek waży 50 kg, a słoń 5 ton i siedzi w odległości 5 m od punktu podparcia. Oblicz jak daleko od punktu podparcia siedzi człowiek, który jest w równowadze ze słoniem.

 

Uwagi eksperta - informacje dla nauczycieli, którzy chcą powtórzyć eksperyment:

Celem doświadczenia jest praktyczne zastosowanie wzoru na dźwignię dwustronną do ważenia przedmiotów. Eksperyment pozwala dostrzec uczniom zależność między masą przedmiotu a długością ramienia dźwigni, na którym umieszczono ważony przedmiot. Przeprowadzenie eksperymentu zgodnie z powyższą instrukcją nie gwarantuje jednak poprawnego wyznaczenia nieznanej masy przedmiotu. Po wykonaniu obliczeń warto zważyć przedmiot i porównać jego masę z otrzymanym wynikiem. W takim przypadku lepiej byłoby zbudować dźwignię o dłuższej belce. W tym celu można posłużyć się  dłuższą  linijką opartą  na ołówku.  Warto także wykorzystać proste przyrządy, które można znaleźć w każdej szkole: wagi laboratoryjne lub statywy, a do pomiarów wykorzystać odważniki.  Przykłady różnych tego typu konstrukcji można znaleźć na stronie WWW pod niżej podanym adresem  http://www.google.pl/search?q=d%C5%BAwignia+dwustronna&hl=pl&rlz=1W1SUNC_plPL364&prmd=imvns&tbm=isch&tbo=u&source=univ&sa=X&ei=EV1CT4T5G8qa-wakhOXnBQ&sqi=2&ved=0CEEQsAQ&biw=1024&bih=540 (data dostępu  20.02.2012 )
Wtedy łatwiej porównać obliczoną i rzeczywistą masę przedmiotu, a uzyskany wynik pozwoli nie tylko zweryfikować poprawność wzoru, ale także  przekona uczniów o jego użyteczności. Należy pamiętać również o tym, że masa i ciężar to pojęcie, których nie można stosować zamiennie.

 

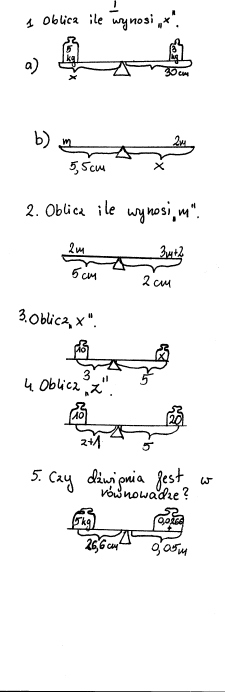Zmienne występujące w doświadczeniu:

1.Jakie zmienną/wielkość będziemy zmieniać? (zmienna niezależna)

Przedmioty do ważenia

2. Jaką zmienną/wielkość będziemy mierzyć - obserwować? (zmienna zależna)

Odległości od punktu podparcia

3. Czego w naszym eksperymencie nie będziemy zmieniać? (zmienne kontrolne)

Przedmiotu o znanej masie do 50g oraz linijki

Proponowany sposób dokumentacji uczniowskiej:

 

Wnioski z doświadczenia

Czy wyniki doświadczenia są zgodne z hipotezą?               TAK  

Uzasadnienie: Potrzebna jest odpowiednia odległość, bo między punktem podparcia
a człowiekiem musi być 500 m.

 

Podstawa programowa

Matematyka

7.   Równania. Uczeń:

  1. zapisuje związki między wielkościami za pomocą równania pierwszego stopnia z jedną niewiadomą, w tym związki między wielkościami wprost proporcjonalnymi i odwrotnie proporcjonalnymi;
  1. rozwiązuje równania stopnia pierwszego z jedną niewiadomą;

6.   Wyrażenia algebraiczne. Uczeń:

  1.  wyznacza wskazaną wielkość z podanych wzorów, w tym geometrycznych i fizycznych.

Fizyka

1.   Ruch prostoliniowy i siły. Uczeń:

  1. wyjaśnia zasadę działania dźwigni dwustronnej, bloku nieruchomego, kołowrotu;

 

Komentarz eksperta

Prawidłowo wykonanie tego doświadczania na lekcji matematyki umożliwia sformułowanie wniosku opisującego związek między wielkościami odwrotnie proporcjonalnymi. Uczniowie powinni zauważyć , że iloczyn wielkości odwrotnie proporcjonalnych jest stały, a więc jeżeli wartość jednej ze zmiennych rośnie k-razy, to wartość drugiej maleje tyle samo, czyli k-razy.